<photo>


Laboratory for Highly Correlated Systems:  Solid State Material Science: Phase Transitions and Transport Properties of Low-dimensional Highly Correlated Conductors

Harukazu Yoshino (Associate Professor)

http://e.sci.osaka-cu.ac.jp/yoshino/ (in Japanese)


1. Current Research and Principal Research Interests

Research Interests
Theme of my research is transport phenomena and phase transitions of low-dimensional and/or highly correlated exotic conductors such as organic superconductors.

Many types of exotic conductors have been synthesized since last century. Organic conductors are one of the examples of such materials as well as high-Tc superconducting oxides. Important key words to understand their interesting physical properties are low dimensionality of electronic system and high correlation between electrons due to relatively small bandwidth because these result in various kinds of novel electronic phases(states). To reveal the chemical and physical properties of the exotic materials, it is important to combine kinds of measurements and to develop theories that explains novel phenomena.

My tools to investigate exotic materials are transport phenomena such as electrical resistivity and thermopower in combination with low temperature, high magnetic field and high pressure techniques. Numerical calculations of transport properties by utilizing recent powerful personal computers are also carried out to understand and predict transport properties of low-dimensional conductors

Followings are my main research topics.
  1. Exploring organic crystals showing high thermoelectric figure of merit ZT.

    When there exists temperature difference between the ends of conducting materials, thermoelectric power is generated between the ends. This phenomenon is known as Seebeck effect. The thermoelectric power is proportional to the temperature difference and the factor is called thermopower or Seebeck coefficient S. This is a kind of power conversion from heat to electricity and has potential applications to utilize waste heat. The efficiency of this power generation is measured by dimensionless thermoelectric figure of merit ZT defined as follows.
    ZT = S2 T/(ρ κ)
    Here T, ρ and κ are absolute temperature, electrical resistivity and thermal conductivity, respectively. Thus we need materials showing large S, low ρ and low κ to achieve high ZT, though it is usually difficult to satisfy every condition.
    In my group we are exploring organic conductors showing high ZT. Organic conductors are potential candidates of thermoelectric materials since most of them have low κ and some of them show large S. To find ideal materials, we are developing systems to measure S, ρ and κ of small (~ 1 mm) and fragile organic conductors, simultaneously.[1,2]
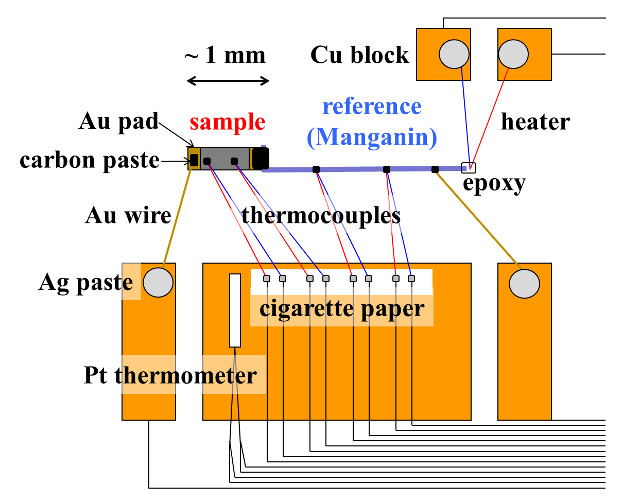
    <figure1> Fig. 1 Schematic view of sample holder to measure electrical resistivity, thermopower and thermal conductivity of small and fragile samples simultaneously.
  2. Angular dependence of magnetoresistance of quasi-one-dimensional (Q1D) conductors

    So-called "Third Angular Effect" (TAE) is what we observed for the first time. This is a phenomenon appearing as a small hump anomaly of magnetoresistance when magnetic field (>5 T) is rotated at low temperature (<4.2 K) within the most conducting plane of one-dimensional metals such as (DMET)2I3. We have also developed a simple way to estimate the anisotropy of Q1D band structure by measuring the width of TAE anomaly. [5-9]
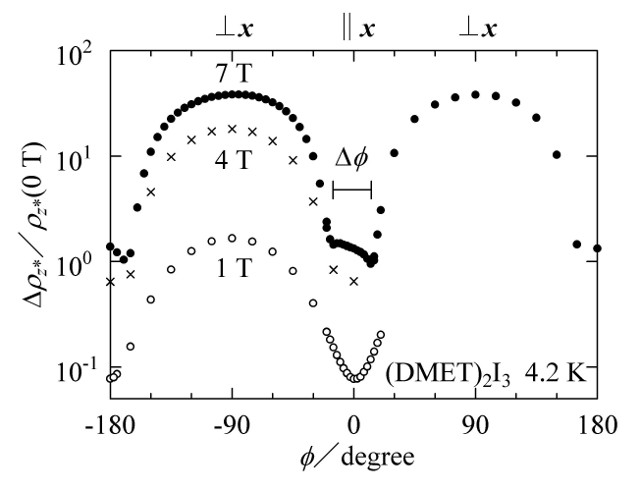
    <figure1> Fig. 2 Third angular effect of magnetoresistance observed for quasi-one-dimensional organic superconductor (DMET)2I3 at 4.2 K.
  3. Phase transitions of organic conductors investigated mainly by measuring electrical resistivity, magnetoresistance and thermopower at ambient and under pressure.

    τ-type organic conductors are a series of quasi-two-dimensional conductors composed of unsymmetrical organic donors such as EDO-S,S-DMEDT-TTF and inorganic monovalent anions like AuBr2-. We have found τ-(EDO-S,S-DMEDT-TTF)2(AuBr2)1+y shows change in the periodicity of angular dependence of magnetoresistance between 90o and 180o depending on how we apply the magnetic field at 1.2 K. This hysteretic behavior of the magnetoresistance is explained by assuming existence of weak ferromagnetic domains, though there is no indication of local spins even at low temperature. [10]
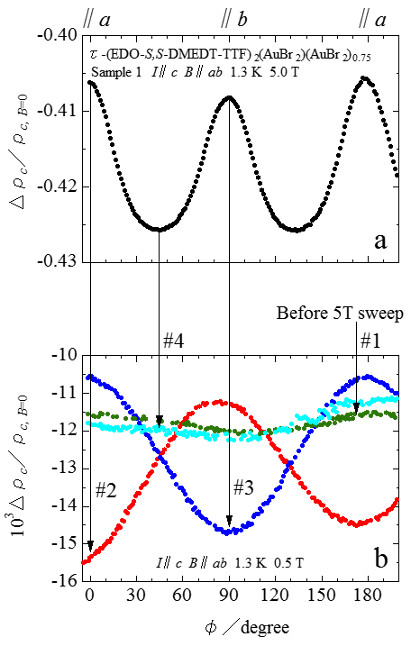
    <figure1> Fig. 3 Hysteretic behavior of field-orientation dependence of magnetoresistance of two-dimensional organic conductor τ-(EDO-S,S-DMEDT-TTF)2(AuBr2)1+y.

Please visit also my homepage for further information on my research as well as other topics such as lecture, my graph software and introduction of orbit elevator.
http://e.sci.osaka-cu.ac.jp/yoshino/(in Japanese)


2. Selected Publications

1. "Thermoelectric and Thermal Properties of Novel &tau-Type Organic Conductors as Thermoelectric Materials", H. Yoshino, H. Nakada, S. J. Krivickas, H. Mori, G. C. Anyfantis, G. C. Papavassiliou and K. Murata, Phys. Status Solidi C, 9, 1193-1195 (2012).

2. "Thermoelectric Figure of Merit of &tau-(EDO-S,S-DMEDT-TTF)2(AuBr2)1+y, (y<0.75) and (TMTSF)2PF6", H. Yoshino, G. C. Papavassiliou and K. Murata, Synth. Met., 159, 2387-2389 (2009).

3. "Evidence of Band-Filling Control of τ-Type Organic Conductors by Thermal Treatment", H. Yoshino, T. Nakanishi, L. Li, K. Murata, D. Graf, E.S. Choi, J.S. Brooks, Y. Nogami and G.C. Papavassiliou, Synth. Met., 153, 453-456 (2005).

4. "Determination of Band-Filling Change in the Two-Dimensional Organic Conductor, τ-(EDO-S,S-DMEDT-TTF)2(AuBr2)1+y by the Quantum Oscillation of Magnetoresistance", H. Yoshino, K. Murata, T. Nakanishi, L. Li, E.S. Choi, D. Graf, J.S. Brooks, Y. Nogami and G.C. Papavassiliou, J. Phys. Soc. Jpn., 74, 417-424 (2005).

5. "Third Angular Effect of (TMTSF)2ClO4 in R- and Q-States under Pressure", H. Yoshino, S. Shodai and K. Murata, Synth. Met., 133-134, 55-56 (2003).

6. "Chemical Pressure Effect on Bandwidth and Dimensionality of Quasi-One-Dimensional Organic Conductors: (DMET)2X, (X = Au(CN)2, AuI2, AuCl2, IBr2, I3, AuBr2 (Z=1) and SCN)", H. Yoshino, K. Murata, K. Saito, H. Nishikawa, K. Kikuchi and I. Ikemoto, Phys. Rev., B 67, 035111/1-9 (2003).

7. "Direct Evidence of Dimensionality Enhancement of Q1D TMTSF and DMET Salts", H. Yoshino, A. Oda, K. Murata, H. Nishikawa, K. Kikuchi and I. Ikemoto, Synth. Met., 120, 885-886 (2001).

8. "Direct Observation of Reconstructed Fermi Surfaces of (TMTSF)2ClO4 Utilizing the Third Angular Effect of Magnetoresistance", H. Yoshino, A. Oda, T. Sasaki, T. Hanajiri, J. Yamada, S. Nakatsuji, H. Anzai and K. Murata, J. Phys. Soc. Jpn., 68, 3142-3145 (1999).

9. "Origin of the Third Angular Effect of Magnetoresistance of Quasi-One-Dimensional Metals", H. Yoshino and K. Murata, J. Phys. Soc. Jpn., 68, 3027-3033 (1999).

10. "Symmetry Change in the Angular Dependence of Magnetoresistance of τ-(EDO-S,S-DMEDT-TTF)2(AuBr2)(AuBr2)y, (y~0.75)", H. Yoshino, K. Iimura, T. Sasaki, A. Oda, G.C. Papavassiliou and K. Murata, J. Phys. Soc. Jpn., 68, 177-180 (1999).