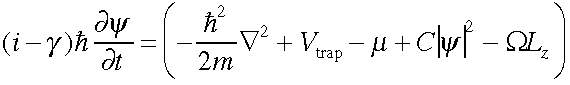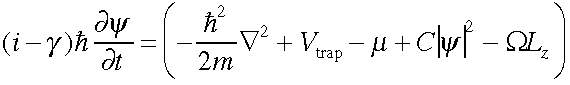アルカリ原子のボースアインシュタイン凝縮体における量子渦格子形成と崩壊のダイナミクス
Kenichi Kasamatsu^{1}, Makoto Tsubota^{1}, and Masahito Ueda^{2}
^{1} Department of Physics, Osaka City University, Sumiyoshi-Ku, Osaka 558-8585, Japan
^{2} Department of Condensed Matter Physics, Tokyo Institute of Technology, Meguro-ku, Tokyo 152-8551, Japan
量子渦は超流動ヘリウムにおいて超流動性に特有の位相欠陥として今まで長く研究されてきた。しかしながら超流動ヘリウムは液体で、比較的高密度であり、その影響による粒子間の強い相互作用のため、このボース流体の理論的取り扱いは困難を極めてきた。さらに実験的にも、量子渦の渦芯のサイズは原子スケールであり、その直接的な観測は現在も達成されていない。しかしながら近年達成されたアルカリ原子のBose-Einstein凝縮体(BEC)は気体であるがゆえに低密度なので、原子間の相互作用が弱く、理論的取り扱いが容易である。また渦芯のサイズも比較的大きくなり、その可視化が可能である。アルカリ原子気体BECの量子渦は最近になっていくつかの実験グループで観測されている[1,2]。
フランスのENSグループではレーザーによって非対称なポテンシャルをつくり、それを回転させる事によってRb原子のBECに量子渦を作る事に成功した。量子渦は回転周波数のある臨界値を超えたところで1本現れる。さらに回転周波数を上げていくと復数本の渦が生成し、規則正しい格子を形成する事が観測された。更にこのグループは量子渦形成の様子を詳しく調べ、渦の核生成は凝縮体の四重極モードの動的な不安定性により引き起こされている事が分かった。閉じ込めポテンシャルの異方的パラメータと回転振動数の値に対して、凝縮体の定常状態は四重極に変形する事やその動的不安定は理論的に調べられている。しかしながらその不安定性の起原やその不安定性がどのように量子渦の形成につながるのかは未解決である。
ここで本研究では以上の事を調べるために、凝縮体が従う運動方程式、Gross-Pitaevskii方程式
,
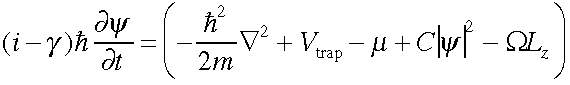を数値的に解く事により、その動的過程を明らかにした。ここで V_{trap} は閉じ込めポテンシャル、 C は粒子間相互作用に比例するパラメータ、 \Omega は回転振動数、\gamma は現象論的に導入した散逸項である。回転のないポテンシャル中での平衡状態を初期状態とし、突如、量子渦が生成する臨界振動数以上の回転を与える状況を考える。まず凝縮体は四重極に変型し、大振幅の振動を始め、その振動は散逸により減衰する徴候が見られた。その後徐々に凝縮体の表面にさざ波が立ちはじめ、それが量子渦のコアへと発展する。四重極変形が元の形に戻ると共に渦は凝縮体の内部へ侵入し、規則正しい渦格子を形成した[3]。
凝縮体密度の時間発展
つぎに凝縮体の位相の時間発展の様子を示す。回転が加わるとすぐに凝縮体の外側の、ほとんど波動関数の振幅が零の領域に$2\pi$の循環を持つ位相の欠陥、すなわち量子渦が現れる。それらは凝縮体の密度がほとんど零の領域に存在する位相場の欠陥であるために、全系のエネルギーや角運動量には何の寄与も及ぼさない架空の量子渦として存在する（我々は`` ghost vortex''と名付けた）。やがてghost vortexは密度がある程度大きな値を持つ凝縮体の表面に到達してひしめき合い、表面波を励起する。系に与える回転振動数に依存して凝縮体の内部に侵入できる渦の数は決まり、系に角運動量を与えるものとして生き残るものと、それ以外は凝縮体の外輪をさまよう。
位相の時間発展
密度と位相の同時時間発展
凝縮体の変形パラメータの時間発展を見ると、渦ができるまでは減衰四重極振動をするが、渦ができるとその振動がなくなり、それと共に全系の角運動量が増大する。これは実験結果と一致する結果を得た。更に回転振動数を徐々に零から非常にゆっくりと上げていく場合を考えると、系は常に平衡状態を保ちつつ発展する。そのとき理論で予言された四重極変形の分枝にそって発展するが、あるところでその分枝を外れて渦を形成する。これは四重極状態の動的不安定性を反映したものであり、実験と一致する結果を得た。
上記の議論で登場した2次の調和振動子ポテンシャルの閉じ込めでは$\Omega$ -> $\omega$で遠心力とキャンセルし、$\Omega$の上限が決まってしまう。しかしながら、2次以上の閉じ込めをを利用すれば$\Omega$の上限がなくなり、高速回転するBECが得られる。次のステップとして2次+4次閉じ込めポテンシャル中のBECに対し、$\Omega$ > $\omega$の回転を与えた時の挙動を2次元Gross-Pitaevskii方程式の数値シュミレーションにより明らかにした[4]。
以下に$\Omega$=2.5$\omega$と$\Omega$=3.2$\omega$におけるダイナミクスを示す。
$\Omega$=2.5$\omega$
density
phase
$\Omega$=3.2$\omega$
density
phase
回転により凝縮体表面にさざ波がたち、それを介して量子渦が外側から凝縮体中に入って格子を形成するが、渦の侵入により凝縮体が回転しだすと、遠心力が働いて凝縮体中央部の密度を下げる。渦間には斥力が働いているので、渦が近付くとエネルギーが上がるが、エネルギーは密度に比例しているために中央では渦の重なりが許され、凝縮体中央部には位相欠陥が集中した「giant vortex」が形成する。位相場を見れば分かるように、位相の特異点は一点で決して重ならず、循環量子数が1以上の多重量子渦とは区別されるものである。
[1]
M. R. Matthews, B. P. Anderson, P. C. Haljan, D. S. Hall, C. E. Wieman, and E. A. Cornell, Phys. Rev. Lett {\bf 83}, 2498 (1999).
K. W. Madison, F. Chevy, W. Wohlleben, and J. Dalibard, Phys. Rev. Lett {\bf 84}, 806 (2000).
J. R. Abo-Shaeer, C. Raman, J. M. Vogels, and W. Ketterle, Science, {\bf 292}, 476 (2001).
E. Hodby, G. Hechenblaikner, S. A. Hopkins, O. M. Marag\'{o}, and C. J. Foot, cond-mat/0106262. etc...
[2]
BECのvortexに関する理論研究のreview論文：A. L. Fetter and A. A. Svidzinsky, J. Phys. Condens. Matter {\bf 13} R135 (2001).
[3]
M. Tsubota, K. Kasamatsu, and M. Ueda, Phys. Rev. A 65, 023603 (2002).
[4]
K. Kasamatsu, M. Tsubota, and M. Ueda, Phys. Rev. A 66 053606 (2002).