Gallery of our numerical simulations

Analysis of the Gross-Pitaevskii equation

  • Spin turbulence

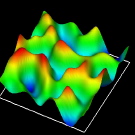
    • We study a spin turbulence in a two-dimensional trapped spin-1 spinor Bose-Einstein condensate by using the numerical calculation of the Gross-Pitaevskii equation. In this calculation, we prepare the helical structure of the spin density vector as the initial state, which leads to the spin turbulence. The file “movie1” shows the　instability of the helical structure in the　early　stage. The file “movie2” shows the dynamics sufficiently after the occurrence of the instability. Then, the spectrum of the spin-dependent interaction energy exhibits the -7/3 power law. We find that the spin density vector at each position points to some direction depending on the position and performs the rapid and fine motion around this direction.

    K. Fujimoto and M. Tsubota, Phys. Rev. A 85, 053641 (2012).


    movie1 movie2

  • Vortex nucleation and transition to binary quantum turbulence in two-component Bose-Einstein condensates

    • We investigate two counter-propagating miscible superflows, in uniform two-component Bose--Einstein condensates. The counterflow becomes unstable in despite of satisfying the miscible condition when the relative velocity exceeds a critical value. Then we investigate the dynamics induced by the instability. The following movie is the numerical result. The blue and red surfaces show the low-density isosurface of component 1 and 2, respectively. The unstable excitations are amplified and then the low-density regions are formed. After that, the regions transform into quantized vortices, which interact and reconnect each other. Eventually, the vortices get tangle.

    Shungo Ishino, Makoto Tsubota, and Hiromitsu Takeuchi, Phys. Rev. A 83, 063602 (2011).


  • Dynamics of vortices and solitons induced by a potential oscillating inside Bose-Einstein condensate

    • We consider that oscillating the Gaussian potential inside a trapped Bose-Einstein condesate(BEC) may be new technique for making quantum turbulence in atomic BECs. As a first step, we study dynamics of vortices and solitons induced by the Gaussian potential by solving numerically the two-dimensional Gross-Pitaevskii equation. Our numerical calculations show that there is synergy dynamics between quantized vortices and solitons. The lower movies are our numerical results.

    Kazuya Fujimoto, Makoto Tsubota, Phys. Rev. A 83, 053609 (2011).

    density
    phase

  • Spin echo in spinor Bose-Einstein condensates

    • We study spin echo in trapped spinor Bose-Einstein condensates by calculating two dimensional Gross-Pitaevskii equations. Spin echo is clearly found in the following movie, showing the dynamics of spin vectors projected on a x-y plane. Just after the 90 degree pulse, the spins are oriented to - y axis, and start precessing on the plane. Then, the precessions gradually diffuse because the Larmor frequency is spatially dependent through the gradient magnetic field. Then, 180 degree pulse is applied, which reverses the direction of the spin. After the pulse, the spins gradually become coherent, eventually refocusing. The dynamics from the dephasing to the rephasing must be spin echo.

    M. Yasunaga and M. Tsubota, Phys. Rev. Lett. 101, 220401 (2008).

  • Numerical simulation of three-dimensional dynamics of vortex lattice formation in a BEC

    • We study three-dimensional dynamics of vortex lattice formation in a rotating ciger-shaped Bose-Einstein condensate through numerical simulations of the Gross-Pitaevskii equation with a phenomenological dissipation term. The three-dimensional simulation reveals unknown dynamical features of the vortex nucleation process, in which the condensate undergoes strongly turbulent stage and the penetrating vortex lines are highly vibrated. They arise from the spontaneous excitation of Kelvin waves on the proto-vortices during the surface wave instability, caused by the inhomogeneity of the condensate density along the elongated axial direction. The left movie shows the time development of the constant surface density and the right does the time development of the constant surface of the superfluid velocity (i.e., vortex lines themselves).

    K. Kasamatsu, M. Machida, N. Sasa and M. Tsubota, Phys. Rev. A 71, 043611 (2005).

  • Kolmogorov spectrum of superfluid turbulence: numerical analysis of the Gross-Pitaevskii equation with the small scale dissipation

    • The energy spectrum of superfluid turbulence is studied numerically by solving the Gross-Pitaevskii equation. We introduce the dissipation term which works only in the scale smaller than the healing length, to remove short wavelength excitations which may hinder the cascade process of quantized vortices in the inertial range. The obtained energy spectrum is consistent with the Kolmogorov law.

    M. Kobayashi and M. Tsubota, Phys. Rev. Lett. 94, 065302 (2005).

  • Kolmogorov Spectrum of Quantum Turbulence

    • Following to above decaying turbulence, we studied steady turbulence by introducing not only dissipation term at small scales but also energy injection term as external potential at large scales to Gross-Pitaevskii equation. We obtained some statistical quantities such as the energy dissipation rate, the energy flux, and the energy spectrum that are consistent with the Kolmogorov law for fully developed turbulence (Movie : Behavior of quantized vortices in fully developed steady turbulence).

    M. Kobayashi and M. Tsubota, J. Phys. Soc. Jpn. 74, 3248 (2005).

  • Multiple domain formation in two-component BECs

    • The dynamics of multiple domain formation caused by the modulation instability of two-component Bose-Einstein condensates in an axially symmetric trap are studied by numerically integrating the coupled Gross-Pitaevskii equations. The modulation instability induced by the intercomponent mean-field coupling occurs in the out-of-phase fluctuation of the wave function and leads to the formation of multiple domains that alternate from one domain to another (shown in the following movie). This behavior is analogous to a soliton train formation, which explains the origin of the long lifetime of the spin domains observed by the MIT group.

    K. Kasamatsu and M. Tsubota, Phys. Rev. Lett. 93, 100402 (2004).

  • Superfluidity of disordered Bose systems

    • We study the two-dimensional superfluidity of disordered Bose systems by anslyzing the Gross-Pitaevskii equation with random potential. We apply the velocity field to the ground state to observe the breaking of superfluidity due to the excitation of vortex pairs above a critical velocity. （Left figure shows the random potential. (Movie) left: condensate density |\Psi|^2, middle: condensate phase, right: normalized rotation of velocity field rot$\vec{v}$）

    M. Kobayashi, M. Tsubota, and T. Iida Physica B 329-333, 210 (2003).

    　

  • Giant vortex formation in a fast rotating BEC

    • A fast rotating Bose-Einstein condensate confined in a quadratic-plus-quartic potential is found to dynamically generate a "giant vortex" that absorbs all phase singularities into a central low density hole, thereby sustaining a quasi-one-dimensional circular superflow at a supersonic speed.（left: condensate density、right: phase）

    K. Kasamatsu, M. Tsubota, and M. Ueda, Phys. Rev. A 66, 053606 (2002)

    rotation frequency Omega=2.5 \omega (trap frequency)
    rotation frequency Omega=3.2 \omega (trap frequency)

  • Vortex lattice formation in a rotating Bose-Einstein condensate

    • We study the dynamics of vortex lattice formation of a rotating trapped Bose-Einstein condensate by numerically solving the two-dimensional Gross-Pitaevskii equation, and find that the condensate undergoes elliptic deformation, followed by unstable surface-mode excitations before forming a quantized vortex lattice. The origin of the peculiar surface-mode excitations is identified to be phase fluctuations at the low-density surface regime. The obtained dependence of a distortion parameter on time and that on the driving frequency agree with the recent experiments by Madison {\it et al.} [Phys. Rev. Lett. {\bf 86}, 4443 (2001)]. （left: condensate density、right: phase）

    M. Tsubota, K. Kasamatsu, and M. Ueda, Phys. Rev. A 65, 023603 (2002)
    K. Kasamatsu, M. Tsubota, and M. Ueda, Phys. Rev. A 67, 033610 (2003)