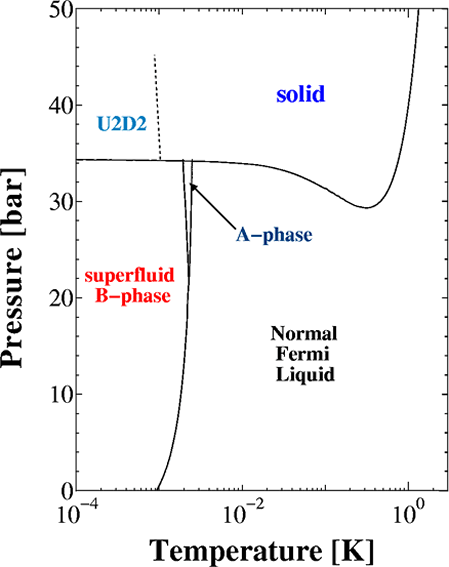
He3 の各論でも述べたとおり、He3 の相図は非常に特長的な形をしている。

固液境界線である融解圧曲線に、負の傾きが存在するのである。そもそも、融解圧 Pm は、クラジウス・クラペイロンの法則という、以下のような熱力学法則に従う。
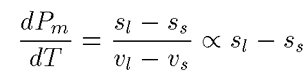 (1)
(1)
ここで、添え字のs と l はそれぞれ固体と液体を示す。vは1モルあたりの体積であるが、温度変化は極めて小さいことが既に解っている。従って、融解圧曲線の傾きは固相液相それぞれのエントロピーSの差に比例する。
通常の固体・液体であれば、エントロピーは固体の方が小さい。だから、融解圧曲線は正の傾きを持つ。しかし、ヘリウム3の場合は量子性が強いために、不思議なことが起きているのだ。まず、液体ヘリウム3は1K以下ではフェルミ縮対しているので、そのエントロピーは温度に比例し、低温になるに従い減少してゆく。しかし、固体ヘリウムは相互作用が小さいため、スピンの自由度だけエントロピーが残っている。
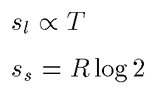
その結果、ある温度で固体と液体のエントロピーが逆転する(すなわち傾きが逆転する)温度がある。この温度こそ融解圧極小点(TM)であり、その圧力を(PM)と呼ぶ(歴史的な経緯により「ポメランチェック・ミニマム」ともいう)。
さて、低温におけるヘリウム3の相図を、モル体積と温度の相図(vT相図)で書き直すと、次のようになる。
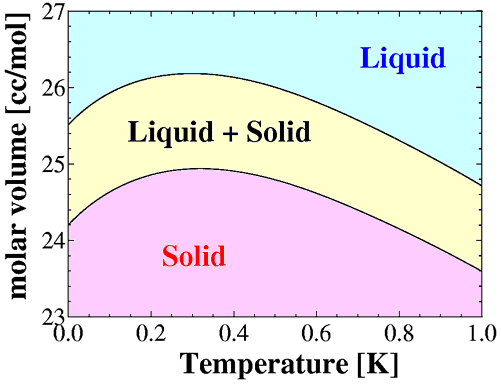
(E.R.Grilly, J.Low Temp.Phys. 4,615,(1971))
すなわち、MCTの中に 27.0 cc/mol だけ仕込んで冷却すると全温度領域において液体のままだが、たとえば25.2 cc/mol (約35気圧)仕込んで冷却すると、0.8K 以下で固液共存状態を実現することができる(PT相図では融解圧曲線上を移動することになる)。固液共存条件さえ成立していれば、融解圧は温度だけに依存し、仕込み圧には依存しなくなる。
MCTの本体は、ダイアフラム型の圧力計である。これは、以下の三つの部品からなる。
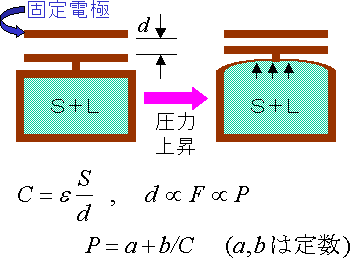
可動電極と固定電極の間の静電容量Cを計測することにより、変位量Δd および圧力P を知ることができる。校正定数a b は、後に述べる。静電容量を計測するので、原理的に発熱がない。また、現在のキャパシタンスブリッヂは00.000001pF程度の分解を持つので、測定には十分な感度を持つ。
さて、高圧チャンバーに、前章で述べた「固液共存圧力」を掛けて冷却すれば、融解圧を知ることができるはずだ。しかし、現実はそう単純ではない。
さて、実際の冷凍器には「希釈冷凍器」でも述べるように、各パーツにおいて時に温度差を付けながら徐々に冷却されてゆく。そして、MCTまでのびるキャピラリ(毛細管:ヘリウム3導入管)も段階的に冷やされてゆく。
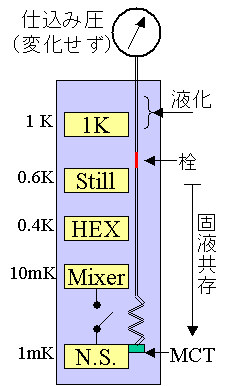 従って、冷凍器の連続運転・定常状態では、固液共存状態にあるMCT(仕込み圧25cc/mol程度)に到達する前(おおむね1Kポット〜STILLの周辺)のキャピラリには固体の栓ができることになる。そして、STILLを通り過ぎる頃にはキャピラリの中で固液共存状態になり、固液比を変えながら最低温度のMCT容器内に達する。(各部の名称および温度については希釈冷凍器の項目参照のこと)
従って、冷凍器の連続運転・定常状態では、固液共存状態にあるMCT(仕込み圧25cc/mol程度)に到達する前(おおむね1Kポット〜STILLの周辺)のキャピラリには固体の栓ができることになる。そして、STILLを通り過ぎる頃にはキャピラリの中で固液共存状態になり、固液比を変えながら最低温度のMCT容器内に達する。(各部の名称および温度については希釈冷凍器の項目参照のこと)
この様に、冷凍器内と室温部との間に「ブロック」が存在するため、MCT内の圧力が変化しようとも、室温部の圧力が変化しようとも、「栓」が融解しない限り、MCT内のヘリウム3は常に「最初に仕込んだ量」を維持している。従って、MCT内を常に「その温度に於ける融解圧力」を保つことができる。これが、キャピラリブロック法である。
MCTの最大の特徴は、自分自身に校正点を持っていることである。以下は、Greywallによって定められた定点である。
| 名称 | 圧力[bar] | 温度[mK] |
| PM | 29.3175 | 318 |
| PA | 34.338 | 2.49 |
| PB | 34.358 | 1.93 |
| PS | 34.39052 | 0.93 |
MCTは圧力計であり、温度掃引により上記4点を通過するとき、チャートレコーダー上に大きな変化が現れる(下の図は小原が物性研在学中に測定したもの)。
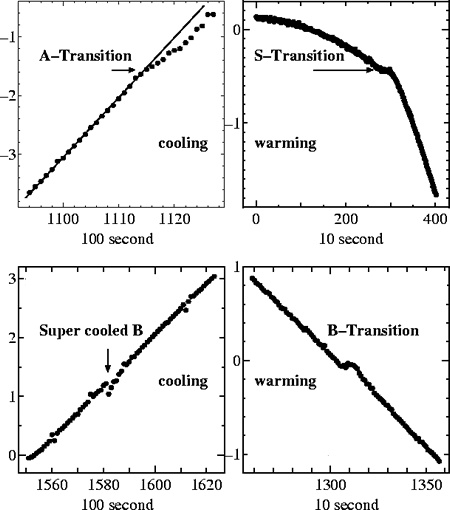
上の図の縦軸は静電容量(任意目盛)、横軸は時間を表す。それぞれが、一定速度の温度掃引を行っていることに注して欲しい。
このほかに、PMは融解圧極小点であり、圧力定点である。
以上のABS(M)点をもちいて、圧力と静電容量の間の関係式を求める事ができる。圧力が求まれば、以下の式を用いて温度を求めることができる。適用可能範囲は、1〜250 mK 程度である。
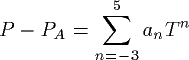
| n | an |
| -3 | -0.19652970E-1 |
| -2 | +0.61880268E-1 |
| -1 | -0.78803055E-1 |
| 0 | 0.13050600 |
| 1 | -0.43519381E-1 |
| 2 | 0.13752791E-3 |
| 3 | -0.17180436E-6 |
| 4 | -0.22093906E-9 |
| 5 | 0.85450245E-12 |
| PA | 34.3380 |
D.S.Greywall Phy.Rev.B33,7529(1986)
これがMCTの原理である。
この様に、MCTはヘリウム3の性質をフルに利用した合理的な温度計である。広い温度範囲で、発熱もなく、再現性もよく、自分自身で校正できるという特徴がある。そのため、極低温における標準的な温度計となっている。