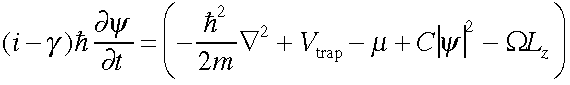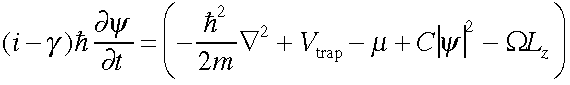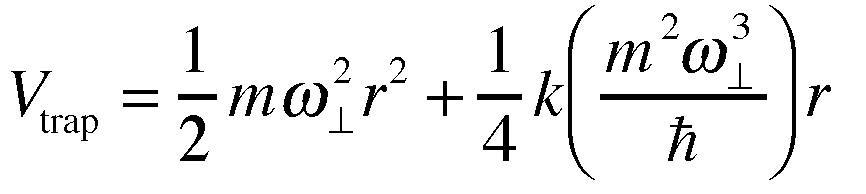Dynamics of vortex array formation in a rotating Bose-Einstein condensate
Japanese version
Kenichi Kasamatsu^{1}, Makoto Tsubota^{1}, and Masahito Ueda^{2}
^{1} Department of Physics, Osaka City University, Sumiyoshi-Ku, Osaka 558-8585, Japan
^{2} Department of Condensed Matter Physics, Tokyo Institute of Technology, Meguro-ku, Tokyo 152-8551, Japan
The recent achievement of Bose-Einstein condensations(BECs) in trapped alkali atomic gases at ultra-low temperatures has stimulated
intense experimental and theoretical activity.
Quantized vortices in the atomic BECs were created experimentally by the groups at JILA, ENS and MIT group.
The motion of a gaseous Bose-Einstein condensate confined in the harmonic trapping potential is described
by the Gross-Pitaevskii equation
,
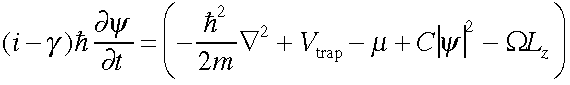where V_{trap} is the external trapping potential, C nonlinear interaction strength, $\Omega$ the rotational frequency,
$\gamma$ represents the effect of a phenomenological disspation.
The first calculation starts with the equilibrium condensate of $C=1400$ trapped in a stationary potential.
The following movies show the typical dynamics of the condensate density $|\psi({\bf r},t)|^2$
after the potential begins to rotate suddenly with $\Omega = 0.7\omega_{\bot}$
density
phase
density + phase
The condensate is elongated along the $x$ axis because of the small anisotropy of $V_{\rm trap}$(Eq.\ (\ref{potential})), and the elliptic cloud oscillates.
Then, the boundary surface of the condensate becomes unstable, exciting the surface waves which propagate along the surface.
The excitations are apt to occur in the surface whose curvature is low, i.e.,parallel to the longer axis of the ellipse.
The amplitude depressions on the waves develop into the vortex cores around which superflow circulates.
Subject to the dissipative vortex dynamics, some vortices enter the condensate, eventually forming a vortex array.
The array formation recovers the axial symmetry of the condensate from its elliptic distortion.
Next, we extend the calculations to the fast rotating regime.
Competing with the centrifugal potential in the limit $\Omega$ -> $\omega$, however, the studies are difficult if the potential is purely quadratic.
Thus, we use the quadratic-plus-quartic potential
,
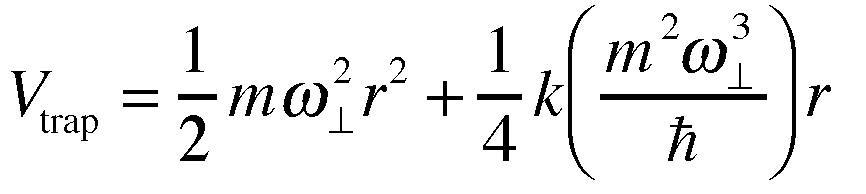studying the dynamics of the condensate after the rotation starts.
The following animations show the time development of the wave function for the fast rotation.
There appears a central region of low density which absorbs the defects.
As the rotation is increased further, the hole absorbs all vortices, making a "giant vortex" with circular flow.
It should be noted that the phase defects do not overlap completely inside the hole, although they are packed closely.
$\Omega$=2.5$\omega$
density
phase
$\Omega$=3.2$\omega$
density
phase
back to the previous page